インダクタ

インダクタとは
インダクタの形状・構造・種類・用途
インダクタの使用上の注意
1. 損失とＱ

インダクタとは

　コンデンサや抵抗器と同じ受動部品で、インダクタも重要な部品です。インダクタと呼んだりコイルと呼んだりします。
　電線をぐるぐる巻かれただけの簡単な構造ですが、電気と密接な磁界を発生させたり、交流成分を阻止したり、共振回路を構成したりと多くの働きがあります。
　導体（導線）に流れる電流によって形成される磁場にエネルギーを蓄えることができる素子です。一般的には電線を渦巻状に巻いた形状をしており、何回も巻くことでアンペールの法則に従いコイル内の磁場が強くなります。そして、ファラデーの電磁誘導の法則に従い、コイル内の磁界の変化に比例して誘導起電力が生じ、レンツの法則に従い、誘導電流は磁界の変化を妨げる方向に流れます。
　インダクタは交流電流を遅延させ再形成する能力があり、時間と共に電圧と電流が変化する部品です。

英語	Inductor
記号	L
単位	H（ヘンリー）

インダクタの形状・構造・種類・用途

　一般的にインダクタの基本的な構造は、導線がコイル状に巻かれたもので、電気エネルギーを磁気エネルギーに変換しインダクタ内部に磁気エネルギーを蓄えることができます。

インダクタの基本構造

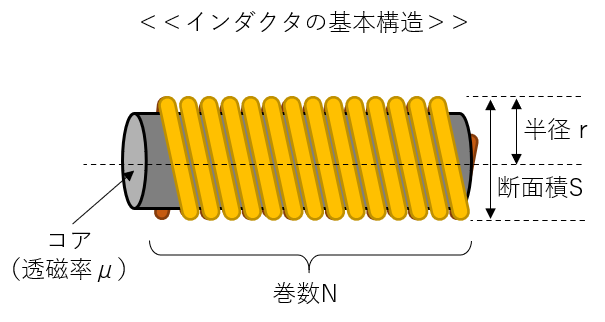
インダクタのインダクタンス
　$$Ｌ=\frac{ｋμＳＮ^2}{l}=\frac{ｋμ(2πr^2)Ｎ^2}{l}$$

Ｌ：インダクタンス[H]
ｋ：長岡係数※
μ ：コアの透磁率[H/m]
Ｎ：コイルの巻き数
Ｓ：コイルの断面積[m²]
ｌ：コイルの長さ[m]

　インダクタは、単純には電線を巻いたものですので、電圧を印加すると基本的に電流が流れます。ただし、電磁誘導による作用を利用する目的の部品であるため、単に電流を流すものではないです。

※長岡係数
　無限長ソレノイドのインダクタンスを求める公式により、有限長ソレノイドのインダクタンスを求められるようにした係数。

直流電源をインダクタに接続した場合

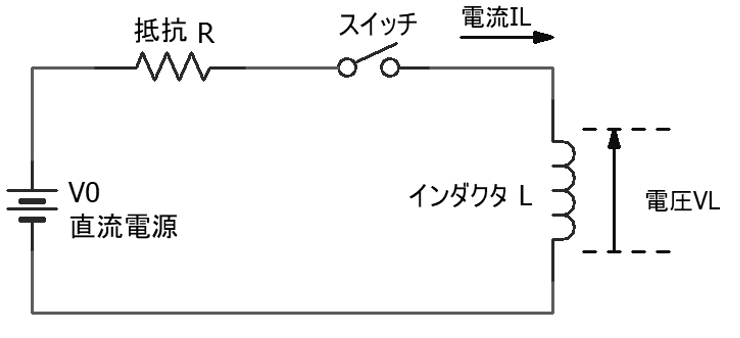
　スイッチによりインダクタに直流電源を印加すると電流が流れ、インダクタに流れる電流の変化により発生する磁束も変化し、インダクタに起電力(誘導起電力)が発生します。
　基本的にインダクタは単独の巻線なので、これを「自己誘導」といいます。この起電力は電流と反対方向に発生し電流の増加を妨げます。逆にスイッチをオフにして電流が減少しようとするとそれを妨げます。

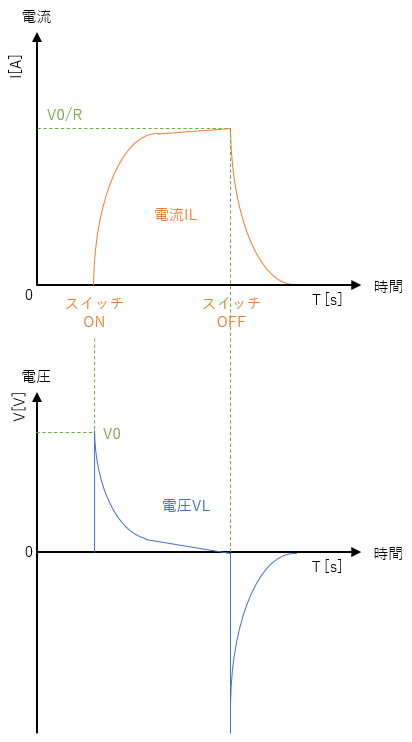
　電流ILは、スイッチオンで流れ出しますが、インダクタの起電力によって増加を妨げられるため、ある時定数を持って立ち上がり、立ち上がった後は抵抗成分に依存して一定電流が流れます。
　スイッチがオフになると電流が立ち下がりますが同じようにある時定数を持ってゼロになることを示しています。

　電圧VLは、スイッチオン時とオフ時のインダクタの起電力を示しています。インダクタに発生する起電力は、式が示すように電流の変化率(ΔI /Δt)に比例します。

　スイッチオン時は上の電流波形のグラフが示すように、ゆっくり電流が増加するので、起電力は電源電圧V0までしか上昇しません。
　スイッチオフ時は電流が瞬時に寸断されるため、オン時に比べ電流の減少が急激で時間あたりの変化率が大きくなることから、より高い起電力が発生します（理論上は∞）。スイッチオフ時に電流が瞬時にゼロにならないのは、インダクタで発生する高電圧の起電圧によってスイッチの端子間で放電電流が流れるためです。

起電力と磁束

インダクタンスは巻線に流れる電流と、巻線と鎖交する磁束数との比で定義される量です。また、巻線に流れる電流の時間変化と巻き線の両端に発生する起電力の比としても表せられます。

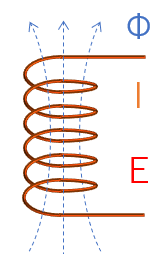
　$\Large{{Φ=Ｌ・Ｉ}}$

　$\Large{Ｅ=Ｌ\frac{ΔＩ}{Δｔ}}$

Φ：鎖交磁束数[Wb]
Ｉ：巻き線の電流　[A]
E：起電力[V]
Ｌ：自己インダクタンス[H]
ΔＩ／Δｔ：電流の変化率[A/s]

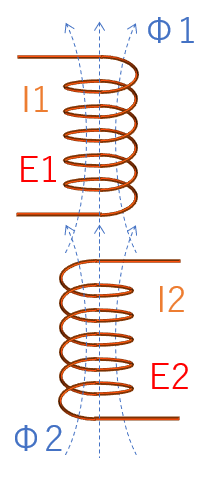
　$\Large{{Φ１=Ｌ１・Ｉ１+Ｍ・Ｉ２}}$

　$\Large{{Φ２=Ｍ・Ｉ１+Ｌ２・Ｉ２}}$

　$\Large{Ｅ１=Ｌ１\frac{ΔＩ１}{Δｔ}＋Ｍ\frac{ΔＩ２}{Δｔ}}$

　$\Large{Ｅ２=Ｍ\frac{ΔＩ１}{Δｔ}＋Ｌ２\frac{ΔＩ２}{Δｔ}}$

Ｍ：相互インダクタンス[H]

インダクタのエネルギー

　$$W=\frac{１}{２}ＬＩ^2$$
Ｗ：エネルギー[J]
Ｌ：インダクタンス[H]
Ｉ：電流[A]

　インダクタは、電気エネルギーを磁気エネルギーに変換し、インダクタ内部に蓄えることができます。
　蓄積できるエネルギーは、左の式で表すことができ、インダクタンスの大きさに比例します。

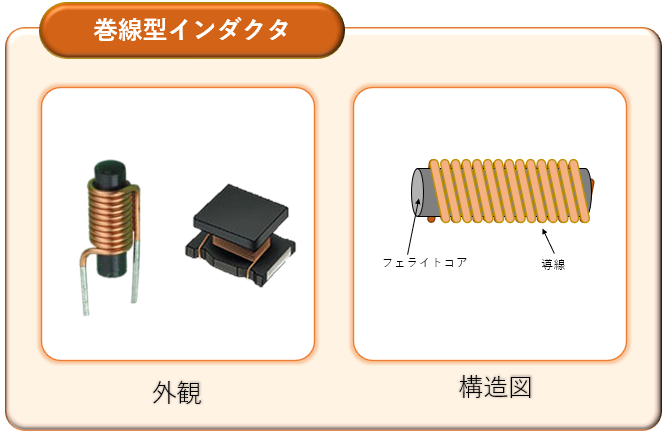
巻線インダクタ

　導線をらせん状に巻いた、コイルの形に最も近いインダクタです。芯（コア）が空洞になっているインダクタもありますが、ミシンで使うボビンのような芯に導線を巻き付けてあるものもあります。用途やインダクタンス値によって、多彩なサイズや形状があります。大きな電流を流さなければならない回路や、高いインダクタンス値が必要な場面に向いています。

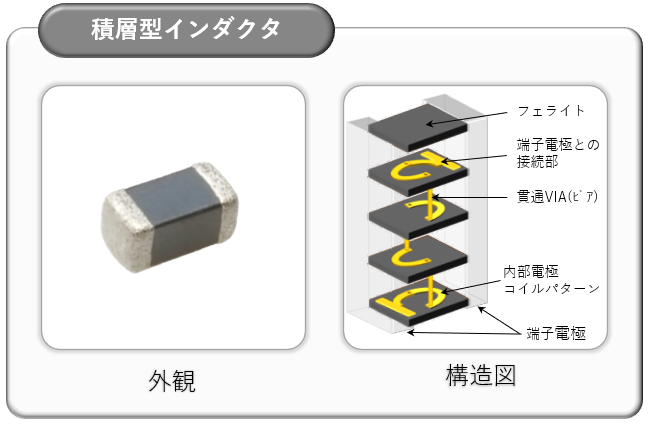
積層インダクタ

　フェライトやセラミックと、コイルパターンを交互に積層したものとなります。コイルパターンは導線を巻くのではなく、フェライトなどの上に導体をスクリーン印刷しています。これを何層も重ねることでコイルのような性質を持たせます。一方でその構造から内部にコンデンサ成分を持つことにもなります。

インダクタの利用方法の分類

インダクタの特性	使用部品・使用回路
電磁石として力が発生するのを利用する。	リレー、ソレノイド
交流電流を阻止するチョークコイルとして使用する。	RFC（高周波チョークコイル）ライン・フィルタ
コンデンサと組み合わせて共振回路として使用する。	同調回路バンドパスフィルタ
2巻線間の相互インダクタンスによりトランスとして使用する。	バラン IFT（中間周波トランス）
インダクタンスにエネルギーが蓄積されるのを利用する。	スイッチングレギュレータ

インダクタの使用上の注意

損失とＱ

　インダクタの損失は、インダクタンスＬに直列な抵抗ｒとして等価的に近が得られています。損失係数をtanδまたはその逆数Ｑで表され、$ｔａｎδ＝\frac{ｒ}{ωＬ}または、Ｑ＝\frac{ωＬ}{ｒ}＝\frac{１}{ｔａｎδ}$の関係にあります。
　インダクタの損失の原因には、巻線の抵抗による銅損、コアに起因する鉄損、構造上発生する分布容量などがあげられます。

銅損

　導体の巻線の抵抗成分によって消費される電力損失のことを言います。流れる電流の2乗に比例して大きくなります。失わるエネルギーは熱となります。
　銅損は負荷損とも呼ばれ、負荷電流の大小によって損失が変化します。よって、抵抗率の低い線材または、太い巻線を使用することが対策となります。
　高周波になると表皮効果により、電流は導体の表面しか流れなくなるため、銀メッキなどを施したパイプなどを使用すると効果が大きくなります。

鉄損

ヒステリシス損：
　磁性材料（代表的には鉄類）のコアを持つインダクタなどのコイルにおいて、そのコアの物性の為に発生する損失のことです。コアの磁区が交番磁界によって磁界の向きを変えるときの損失です。言い換えると、コア内磁束の大きさや方向の変動により、コア中の磁気分子の方向・配列が変化します。この変化の時に分子相互間の摩擦損を生ずることによるもので、ヒステリシスループの囲む面積に比例します。

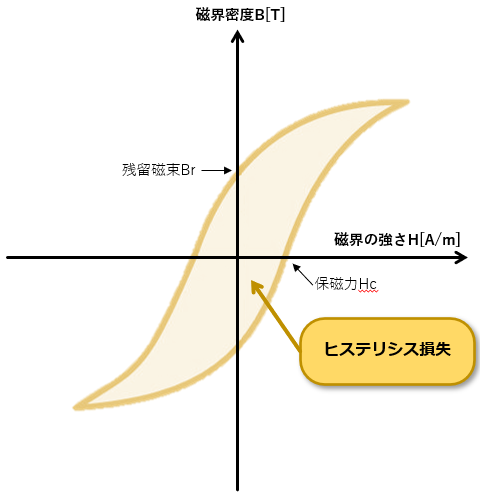
ヒステリシス損
$\Large{Ｐ_{ｈ}＝ｋ_{ｈ}ｆＢ_{ｍ}^２＝ｋ’\frac{Ｖ^{２}}{ｆ}}$

$Ｐ_{ｈ}：ヒステリシス損\\
Ｖ：電圧[V]\\
ｆ：周波数[Hz]\\
ｋ_{ｈ}、ｋ’：比例係数\\
Ｂ_{ｍ}：最大磁束密度[T]$

うず電流損：
　導体の一部で磁束が変化したり、または磁束が導体を横切ったりすると、電磁誘導作用によって、その導体内部に起電力を誘起しその部分だけ電流が流れる。この電流をうず電流という。うず電流が流れると、その通路は抵抗をもっているので電力損失を生じてジュール熱を発するため温度が上昇するときの損失です。

残留損：
　残留損失は、実態としては非常に分かりにくいものです。磁気の粘性によって生じるものとされていますが、磁気粘性はコア材内部の磁界と磁束の時間的なズレによって生じると考えます。つまり、磁界と磁束密度の位相のズレと解釈できます。磁界と磁束密度の位相のズレは透磁率の変化にも関わるため、残留損失自体を測定することは不可能です。
　そのため、ヒステリシス損失でもなく、渦電流損失でもないものをひと括りにして、残留損失として扱うことが多いです。

分布容量

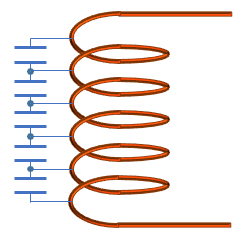
　インダクタの巻線間に存在する静電容量であり、周波数によりインダクタンスと共振現象を生じます。
　このため、ある周波数では動作しなくなったりして好ましくありません。

この分布容量を無くすには、
　（１）多層に巻く場合、巻き始めと巻き終わりを近接させない。
　（２）透磁率の大きいコアを用いて巻き数を減らし、巻線の間隔を広げる。